这篇文章我们将讲解一下机器学习与数据挖掘领域最常用的一些算法,包括有监督学习的分类与回归算法以及无监督学习的聚类与降维算法。好了,闲话不多说,让我们一起开始吧!
K-Nearest Neighbor(K近邻)
前置假设
- 输入空间: $\chi \subseteq \mathbb R^n$
- 训练集: $T = [(x_1,y_1),(x_2,y_2),…,(x_N,y_N)]$
- 输出空间: $\gamma = [c_1,c_2,…,c_k]$
K近邻算法基本思想
K近邻算法并不具有显式的学习过程,K近邻算法实际上是利用训练集数据对特征空间进行划分,并作为其分类的模型。给定一个训练集,对于新的输入实例,首先在训练集中找到与该实例最近的K个实例,然后统计这K个实例的多数属于哪个类,就把该实例划分为哪个类。
K近邻算法的三个要素
经过上面的讨论,我们可以总结出K近邻算法的三个要素:
- K值的选择
- 距离的度量
- 分类决策的准则
K值的选择
首先考虑一个极端的情况,当K值为1时,此时的K近邻算法又称为最近邻算法,这种情况下,很容易发生过拟合,很容易将一些噪声学习到模型中(很容易将实例判定为噪声类别)
我们再考虑另外一种极端情况,当K值为N时,此时不管你输入的实例是什么类别,最终的模型都会将该实例判定为模型中实例最多的类别。也就是在这种情况下,很容易发生欠拟合。
距离的度量
- 闵可夫斯基距离
- 曼哈顿距离
- 欧氏距离
- 切比雪夫距离
设有两个向量:
$$x_i = (x_{i}^{(1)},x_{i}^{(2)},x_{i}^{(3)},…,x_{i}^{(n)})$$
$$x_j = (x_{j}^{(1)},x_{j}^{(2)},x_{j}^{(3)},…,x_{j}^{(n)})$$
闵可夫斯基距离的定义如下:
$$d_{(x_i,x_j)} = (\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^p)^{1 \over p}$$
当 p=1 时就是曼哈顿距离,当 p=2 时就是欧氏距离,当 p=$\infty$时就是切比雪夫距离。
分类决策的准则
这利用的是多数表决的决策准则,关于对多数表决规则的解释可以参考《统计学习方法》这本书的3.2.4小节(多数表决规则等价于经验风险最小化)
特征归一化
为了让各个特征在分类的时候同等重要,我们需要将各个特征进行归一化。
对异常值敏感
由于KNN是基于距离的算法,所以KNN对异常值是比较敏感的。
Linear Regression(线性回归)
定义符号
假设数据集为:{$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})$},参数为$\theta$,其中:
- 训练样本数目为 m
- 第 i 个样本为$(x^{(i)},y^{(i)})$
- $x^{(i)} = [x_1^{(i)},x_2^{(i)},…,x_n^{(i)}]^T, x^{(i)} \in \mathbb R^n$
- $y^{(i)} \in \mathbb R$
- $\theta = [\theta_1,\theta_2,…,\theta_n]^T, \theta \in \mathbb R^n$
假设函数
$$h(x) = \sum_{i=1}^n \theta_ix_i = \theta^Tx$$
目标函数
目标函数的形式
$$J(\theta) = {1 \over 2m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2$$
为什么要选择这样的目标函数?
(1) 对于每一个样例$(x^{(i)},y^{(i)})$, 假设预测值和真实值存在以下关系:
$$y^{(i)} = {\theta}^Tx^{(i)} + {\epsilon}^{(i)}$$
其中${\epsilon}^{(i)}$表示预测值和真实值之间的差值。
(2) 影响误差的因素有很多,这些因素又都是随机分布的。根据中心极限定理,许多独立随机变量的和趋于正态分布。所以进一步假设:
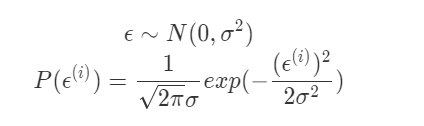
当给定参数$\theta$和变量$x$时,有以下公式成立:
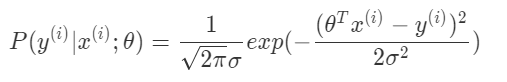
(3) 再进一步假设各个样例的误差是独立同分布的,可以得到似然函数:
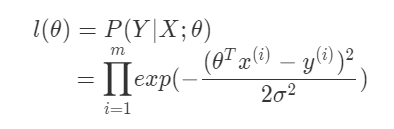
因为似然函数表示的是在参数$\theta$下数据集出现的概率,所以需要做的工作就是极大化似然函数。
(4) 将似然函数转化为对数似然:
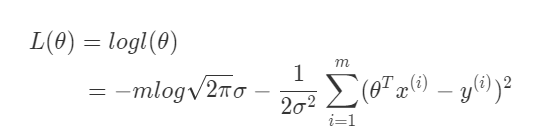
转换为对数似然函数后,需要做的工作也转变为极大化对数似然函数,要极大化对数似然函数,从式子中可以得出需要使得$\sum_{i=1}^m(\theta^Tx^{(i)} - y^{(i)})^2$最小。到这一步也基本可以对选择这样的目标函数做出一个比较合理的解释了。
优化目标函数的方法
批量梯度下降
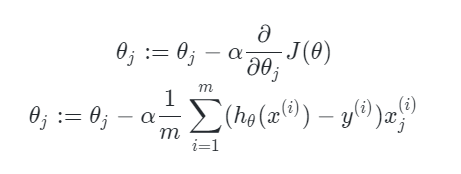
随机梯度下降
当每次只用一个样本训练时,$J(\theta)$退化成以下形式:
$$J(\theta) = (h_\theta(x^{(i)})-y^{(i)})^2$$
此时参数更新公式变为以下形式:
$$\theta_j:= \theta_j - \alpha(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$
随机梯度下降(Stochastic Gradient Descent)可能永远不能收敛到最小值,参数$\theta$将会一直在使得$J(\theta)$取最小值的附近振荡。
K-means(K-均值聚类)
假设
K-means算法是一种聚类算法。为了更好的解释这个算法,首先我们假设给定的数据集为$(x^{(1)},x^{(2)},…,x^{(m)}),x^{(i)} \in \mathbb R^n,$, 注意数据是没有标签的。
K-means算法的一般流程
- 选择初始的K个聚类中心$\mu_1,\mu_2,…,\mu_k \in \mathbb R^n$
- 重复以下两步直到收敛(聚类中心不再变化或者变化低于阈值):
(1). 计算每个样本到各个聚类中心的距离,并将其类别标号设为距其最近的聚类中心的标号,即:
$$c^{(i)}:=arg\min_{j}||x^{(i)}-\mu^{(j)}||^2, j = 1,2,…,k$$
其中$c^{(i)}$为第i个样例的类别标号
(2). 更新聚类中心的值为相同类别的样本的平均值:
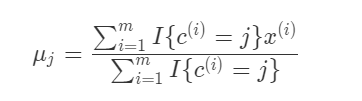
其中,当$c^{(i)} = j$时,$I{c^{(i)}=j} = 1$,当$c^{(i)} \ne j$时,$I{c^{(i)}=j} = 0$
对K-means算法的进一步解释
- K-means算法要优化的目标函数如下:
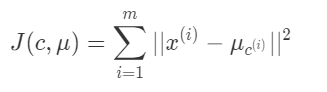
优化目标可以看成让所有点到其对应的聚类中心点的距离和最小。K-means算法可以看成对目标函数J的坐标下降过程,对应的解释如下:
- 执行上述2(1)这一步的时候,相当于固定$\mu$,改变$c$ (每个样本所对应的类别),改变的规则是样本到哪个聚类中心的距离最小就将对应的样本对应的$c$改为哪类,所以$J(c,\mu)$一定会减小。
- 执行上述2(2)步的时候,相当于固定所有样本的$c$,重新计算各个类别的中心,进一步使得$J(c,\mu)$减小。
- 目标函数$J$不是一个凸函数,因此K-means算法不能保证收敛到全局最优解,一个简单的方法就是随机初始化多次,以最优的聚类结果作为最终的结果。
- 聚类结束后,如果一个中心没有任何相关的样本,那么这个中心就应该去掉,或者重新聚类。
对K-means算法的改进
- K-means++算法对K个初始聚类中心的选取做了改进,各个聚类中心之间的距离越远越好。
(1) 随机选取一个聚类中心
(2) 计算每个样本到所有已知聚类中心的最短距离$D(x)$
(3) 计算每个样本被选为下一个聚类中心的概率${D^2(x)}\over{\sum_{x \in X}D^2(x)}$
(4) 确定每个样本被选为下一个聚类中心的概率区间
(5) 生成一个0~1的随机数,选取随机数对应区间的样本作为下一个聚类中心
(6) 重复以上过程,直到选取了K个聚类中心
- 二分K-means算法,为了克服K-means聚类算法容易陷入局部最小值的问题和提高聚类的性能,提出了二分K-means聚类算法。该算法的基本思想是首先将所有的样本点划分到一个簇,然后将该簇一分为二,之后选择其中的一个簇继续进行划分,直到得到用户指定的簇数目为止。选择哪个簇进行划分取决于对其划分是否可以最大程度的降低SSE(误差平方和)
K值的选取
对于如何选取K值,本文只简要提及以下两种方法:
- 经验法
- 手肘法:横坐标为K值,纵坐标为所有样本点到它所对应的聚类中心的误差平方和,在图中找到最佳拐点。
Principal Components Analysis(主成分分析)
定义符号
主成分分析(Principal Components Analysis,PCA)是一种降维方法。为了更好地解释该算法,首先假设数据集为$(x^{(i)};i = 1,2,…,m)$, 其中$x^{(i)} \in \mathbb R^N$, 也就是说数据集一共包含m条数据,每条数据的特征向量维度为n.
中心化和标准化
中心化又叫零均值化,中心化(零均值化)后的数据均值为零。下面两幅图是数据做中心化前后的对比,可以看到其实就是一个平移的过程,平移后所有数据的中心是(0,0)。
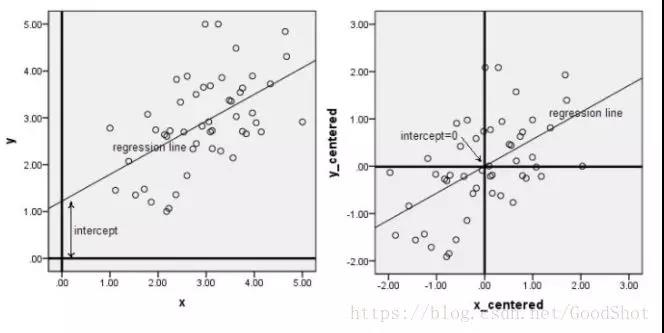
数据标准化的目的就是使各个特征都在同一尺度下被衡量。
Z-score标准化
Z-score标准化(也叫0-1标准化),这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。进过处理的数据符合正态分布,即均值为0, 标准差为1。Z-score标准化的公式如下:
$$x^* = {x-\mu \over \sigma}$$
我们可以发现Z-score标准化的过程中是包含中心化的。以下图片展示了一组数据进行Z-score标准化的过程。左图表示的是原始数据,中间的是中心化后的数据,右图是将中心化后的数据除以标准差,得到的标准化后的数据,可以看出每个维度上的尺度是一致的(红色线段的长度表示尺度)。
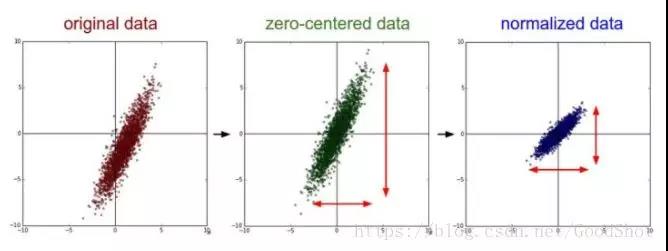
想要使用PCA算法,需要先对数据做以下处理:
- $\mu = {1 \over m}\sum_{i=1}^mx^{(i)}$
- $x^{(i)} = x^{(i)} - \mu$
- $\sigma_j^2 = {1 \over m}\sum_i(x_j^{(i)})^2$
- $x_j^{(i)} = {x_j^{(i)}\over \sigma_j}$
整个过程其实就是Z-score标准化的过程
PCA算法的基本思想
PCA算法的基本思想就是寻找到数据的主轴方向,我们希望数据在主轴方向上能够更好地被区分开,直观的说就是我们希望数据在主轴方向上尽量分散,更具体的就是指所有的点在主轴方向的投影点的方差最大。比如在以下两个图中,在方向一上,数据更分散,投影点的方差最大,所以如果从这两个方向上选一个主轴的话,应该选择方向一。
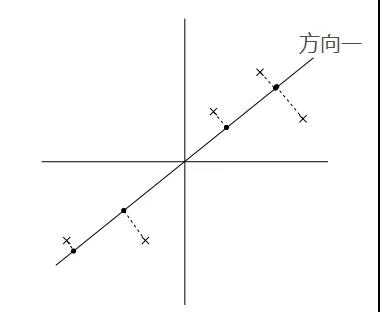
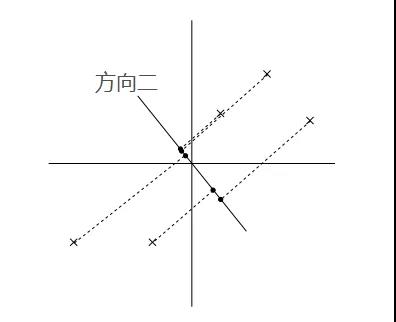
在数据已经做了Z-score标准化的前提下,数据的均值为0,其投影点的均值也为0.
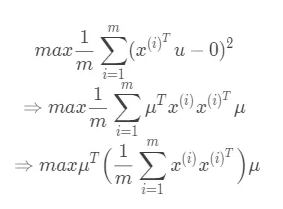
(1) 上述第一个式子里面的$x^{(i)^T}\mu$就是$x^{(i)}$这个向量在投影方向$\mu$上的长度。这里的$\mu$是单位向量,即$||\mu|| = 1$。
(2) 上述第二个式子是把向量内积的平方换了一个写法。
(3) 上述第三个式子又对式子做了一个变形,不难看出${1 \over m}\sum_{i=1}^mx^{(i)}x^{(i)^T}$是一个矩阵,并且这个矩阵是对称矩阵(实际上是一个协方差矩阵)。
(4) 纵观整个式子,最终的目标则是找到使得整个式子取到最大值的向量$\mu$,所以这是一个最优化问题。
求解$\mu$与降维
$\mu$是一个单位向量,这其实是这个最优化问题的约束条件($||\mu|| = 1$), 可以使用拉格朗日方程来求解最优化问题:
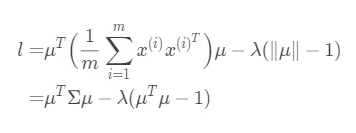
对$\mu$求导:
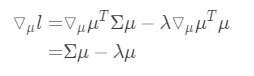
令导数为0,可以发现$\mu$是$\Sigma$的特征向量。再因为矩阵$\Sigma$是对称矩阵,所以一定能找到n个相互正交的特征向量,如果要选出k个主轴方向,我们从n个特征向量里面选出k个最大的特征值对应的特征向量即可。假设选出的k个特征向量为:
$${\mu_1,\mu_2,…,\mu_k}$$
则可以通过以下公式将原来的n维的$x^{(i)}$降为k维的$y^{(i)}$:
$$[y_1^{(i)},y_2^{(i)},…,y_k^{(i)}] = [\mu_1^Tx^{(i)},\mu_2^Tx^{(i)},…,\mu_k^Tx^{(i)}]$$
Logistic Regression(LR—逻辑回归)
推导过程
假设要解决的问题是一个二分类问题,目标值为{0,1},以线性回归为基础,将模型输出映射到[0,1]之间。我们选择这样一个函数:
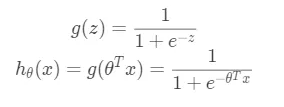
其中$g(z)$被称为sigmoid函数。为什么要选择sigmoid函数其实是可以通过指数分布族加上广义线性模型进行推导分析的。通过sigmoid函数我们可以计算单个样本属于正类还是负类的概率:
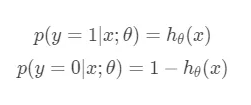
我们将上面两个式子合并成一个:
$$p(y=x|;\theta) = (h_\theta(x))^y(1 - (h_\theta(x))^{(1-y)}$$
有了上面这个式子,我们就能很容易的得到函数$h$在在整个数据集上的似然函数:
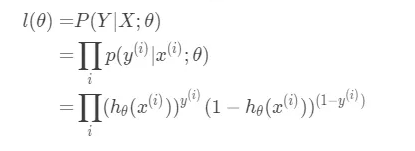
将其转为对数似然函数:
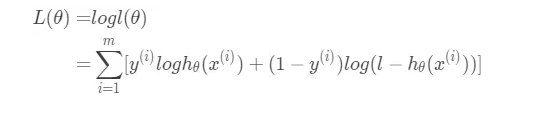
假设我们用随机梯度下降法更新参数,每次只用一个样例,则上面的对数似然函数退化成:
$$L(\theta) = y^{(i)}logh_\theta(x^{(i)}) + (1 - y^{(i)})log(1 - h_\theta(x^{(i)}))$$
更新参数的公式为:
$$\theta_j:= \theta_j + \alpha * {\partial\over\partial\theta_j}L(\theta)$$
这里的$\alpha$就是学习率。其次注意式子里面的“+”,因为我们要极大化对数似然函数,所以我们需要沿着梯度方向更新参数。接下来我们要做的就是求出$L(\theta)$对各个参数的偏导。
- 首先我们知道sigmoid函数的求导结果为:
$$g’(z) = g(z)(1 - g(z))$$
- 我们可以推导出$L(\theta)$对各个参数的偏导为:
$${\partial\over\partial\theta_j}L(\theta) = x_j(y - h_\theta(x))$$
- 所以,参数更新公式为:
$$\theta_j:= \theta_j + \alpha(y^{(i)} - h_{\theta_j}(x^{(i)}))x_j^{(i)}$$
如果我们用梯度下降法,每次更新参数用所有样例,则参数更新公式为:
$$\theta_j:= \theta_j + \sum_{i=1}^m\alpha(y^{(i)} - h_{\theta_j}(x^{(i)}))x_j^{(i)}$$
Naive Bayes(朴素贝叶斯)
判别式学习算法和生成式学习算法
对于一个分类问题来说(这里以二分类问题为例),逻辑回归算法是在解空间中寻找一条直线从而把两种类别的样例分开,对于新的样例只要判断其在直线的哪一侧即可,这种直接对问题求解的方法可以称为判别式学习方法。生成式学习算法则是对两个类别的数据分别进行建模,用新的样例去匹配两个模型,匹配度较高的作为新样例的类别。
贝叶斯公式
朴素贝叶斯算法的核心自然是贝叶斯公式:
$$P(B|A) = {P(A|B)P(B) \over P(A)}$$
在机器学习分类算法中,用以下形式可能会更加清晰明了:
$$P(类别|特征) = {P(特征|类别)P(类别) \over P(特征)}$$
朴素贝叶斯算法的基本思想
- 如果要解决的是一个分类问题,那么我们的任务就是根据样本的特征来判断样本属于哪个类别。首先我们要对训练集中的样本进行统计,并计算各个类别数据所占的比例(先验概率):
$$P(类别y)$$
- 接着计算各个类别下各个特征取到某值的概率(条件概率):
$$P(第i个特征的第K个可取值|类别y)$$
- 朴素贝叶斯算法假设各个特征相互独立,这样的话,对于测试集上的一个新样本来说,有以下等式成立:
$$P(特征1,特征2,…,特征n|类别y) = P(特征1|类别y)P(特征2|类别y),…,P(特征n|类别y)$$
- 给定测试集上的一个样本(也就是告知样本的各个特征的取值),我们可以计算出:
$$P(特征|类别y)P(类别y)$$
- 想要计算出后验概率P(类别y|特征),我们还需要计算出P(特征),但是任一样本的P(特征)在各个类别下的值是完全相同的,又因为我们的目的是找出样本属于哪个类别的概率最大,为了简化计算,分母部分的的P(特征)可以去掉。
拉普拉斯平滑
$P(特征1|类别y)P(特征2|类别y),…,P(特征n|类别y)$中有任何一部分的值为0,则整个式子的值为0。在对条件概率P(特征i的第k个可取值|类别y)进行建模时,发现它们很有可能为0,为了避免出现这种情况,可以引入拉普拉斯平滑,在建模过程中,假定每个特征的每个取值至少出现1次,这样:

实例
某个医院早上收了6个门诊病人,如下表:
| 症状 | 职业 | 疾病 |
|---|---|---|
| 打喷嚏 | 护士 | 感冒 |
| 打喷嚏 | 农夫 | 没患感冒 |
| 头痛 | 建筑工人 | 没患感冒 |
| 头痛 | 建筑工人 | 感冒 |
| 打喷嚏 | 教师 | 感冒 |
| 头痛 | 教师 | 没患感冒 |
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
- 根据贝叶斯公式可得:
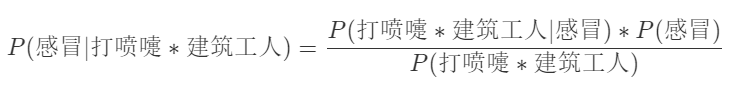
- 假定“打喷嚏”和“建筑工人”这两个特征是相互独立的,因此,上面的等式就变成了:

- 按照以上公式进行统计、计算:

- 那他没患上感冒的概率为0.33,我们可以通过以下式子进行验证:

Desicion Tree(决策树)—Part 1
决策树算法简介
决策树算法既可以应用于分类问题,也可以应用于回归问题。决策树算法有可解释性好、分类速度快的特点。决策树算法主要包含特征选择、决策树的生成、决策树的修剪这几个主要步骤。决策树相关的算法原理主要包含ID3、C4.5、CART,其中scikit-learn使用了优化版的CART算法作为其决策树算法的实现。
数据集
给出以下数据集,考虑如何利用这个数据集建立一棵决策树,当给定一个新的西瓜,这棵决策树可以利用这个西瓜的特征(色泽、根蒂、敲声、纹理、脐部、触感)来尽量准确的判断这是不是一颗好瓜?
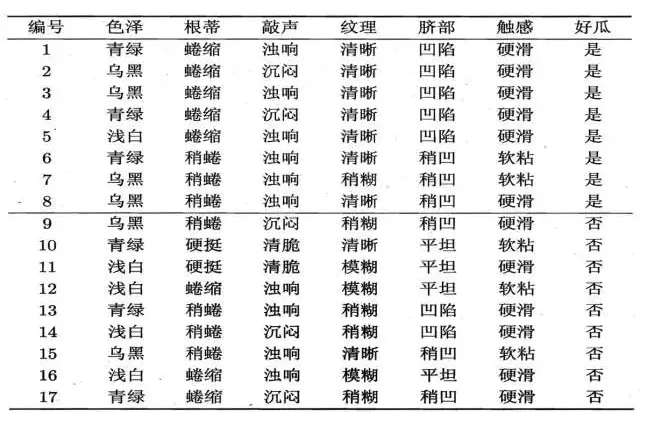
决策树模型
决策树模型由结点和有向边组成,结点又包括内部结点和叶子结点。内部结点表示一个特征(也可以叫属性),叶子结点表示一个类别。
特征选择
决策树学习的关键就是特征选择的问题,即如何确定每个内部结点对应哪个特征(每次划分应该按照哪个特征来进行)。
信息熵
在信息论中,熵是对随机变量不确定性的度量。随机变量的不确定性越高,它的熵就越大。设随机变量$X$是一个取有限个值的离散的随机变量,其概率分布为:
$$p(X = x_i) = p_i, i=1,2,…,n$$
随机变量的熵定义为:
$$H(X) = -\sum_{i=1}^np_ilogp_i$$
若$p_i = 0$则定义:
$$0log(0) = 0$$
当$log$函数以2为底时,这时的熵被称为比特熵,当$log$函数以$e$为底时,这时的熵被称为纳熵。我们可以用熵来度量一个数据集的混乱程度。
信息增益
假设离散特征(属性)$a$有$V$个可能的取值${a^1,a^2,…,a^V}$,若用特征$a$对样本集$D$进行划分,则会产生$V$个分支节点,其中第$V$个分支结点包含了样本集$D$中的所有在特征(属性)$a$上取值为$a^V$的样本,记为$D^v$.
首先可以计算出所有$D^v$的熵。然后我们假设 $|D^v|$表示的是$D^v$中的样本数量,$|D|$表示的是$D$中的样本数量,这样我们可以通过计算给每个分支结点赋予一个权重:
$$|D^v|\over|D|$$
接着我们就可以计算出样本集$D$按照特征$a$划分的信息增益:
$$Gain(D,a) = G(D,a) = H(D) - \sum_{v=1}^V{|D^v|\over|D|}H(D^v)$$
一般来说信息增益越大,说明按对应特征将数据集进行划分后,数据集的混乱程度下降的越多。
ID3算法实例介绍
ID3算法就是根据信息增益来选择特征进行划分的。按照一个特征进行划分后,产生的信息增益最大,ID3算法就选择该特征进行划分。
假设上文给出的数据集为$D$,观察数据集只有两类,正例个数为$8$,负例个数为$9$。我们设$p_1$为样本集中正例的概率,$p_2$为样本集中负例的概率,熵采用比特熵的计算方式,则:
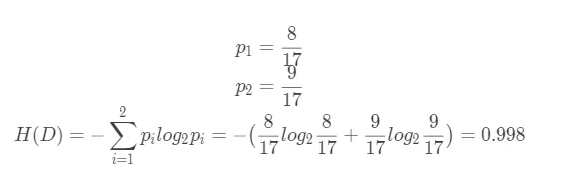
接下来考虑按照色泽进行划分,色泽这个特征对应三个取值:{青绿、乌黑、浅白},如果使用这个特征进行划分,那么会得到三个分支结点。也就是会得到三个子样本集合,分别记为: ${D^1,D^2,D^3}$, $D^1$对应色泽为青绿的子集,$D^2$对应色泽为乌黑的子集,$D^3$对应色泽为浅白的子集。
$D^1$包含 6 个样本,3 个正例,3 个反例。
$D^2$包含 6 个样本,4 个正例,2 个反例。
$D^3$包含 5 个样本,1 个正例,4 个反例。
计算$D^1,D^2,D^3$三个划分后的样本集的权重和熵,设$D^1,D^2,D^3$对应的权重分别为$p_1,p_2,p_3$.

然后我们用同样的方法,依次计算按照其他特征(根蒂、敲声、纹理、脐部、触感)进行划分对应的信息增益:
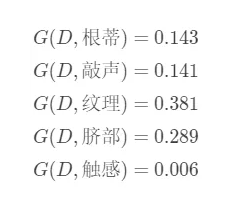
通过比较我们可以确定通过纹理这个特征进行划分,得到的信息增益最大,所以应该选择纹理这个特征进行划分。划分结果如下:
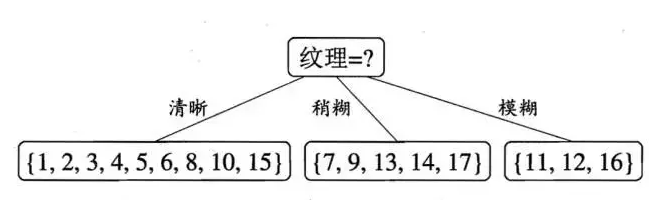
接着对得到的三个子数据集$D^1,D^2,D^3$进行划分。子数据集$D^1$中有 9 个样例,有色泽、根蒂、敲声、脐部、触感五个特征可供选择($D^1,D^2,D^3$这三个子数据集中每个数据集的纹理特征经过第一次划分已经是唯一的了)。划分$D^1$数据集,计算按各个特征进行划分对应的信息增益:

经过比较我们发现按根蒂、脐部、触感三个特征中的任意一个划分,信息增益都能取到最大值0.458,我们可以从这三个特征里任选一个进行划分。这里选择根蒂这个特征进行划分。如此按照递归的方式依次对各个子数据集进行划分最后不难得到一棵如下的决策树:
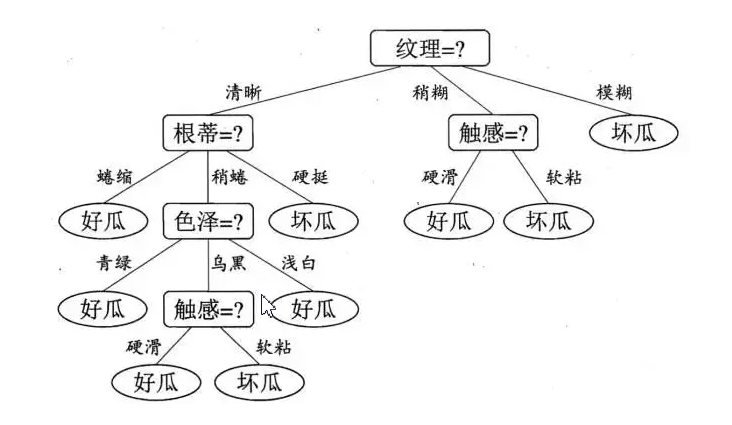
ID3算法整体过程
算法的输入的是包含$m$个样本的数据集$D$,每个样本有$n$个离散特征,特征集为$A = {A_1,A_2,…,A_n}$, 最终输出为决策树$T$。
1 | (1) 初始化信息增益的阈值ϵ |
ID3算法的不足之处
- ID3算法没有考虑取值为连续值的特征
- ID3算法对可取值较多的特征有偏好
- ID3算法没有处理缺失值
- ID3算法没有考虑过拟合的问题
Desicion Tree(决策树)—Part 2
上一部分提到ID3算法有四个不足之处,这 4 个不足之处在C4.5算法中得到了改进。
处理连续特征
ID3算法没有考虑连续特征,比如质量,密度等,C4.5算法的思路是将连续的特征离散化。假设在样本集$D$中连续特征$a$的取值有$n$个,记为 ${a_1,a_2,a_3,…,a_n}$。那么对于特征$a$一共有$n-1$个候选划分点,首先将这$n$个点排序,然后通过下式计算出这$n-1$个候选点:
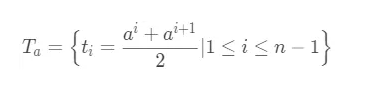
对于这$n-1$个点,分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为$a_i$,则小于$a_i$的值为类别1,大于$a_i$的值为类别2,这样我们就做到了连续特征的离散化。要注意的是,与离散属性不同的是,如果当前节点为连续属性,则该属性后面还可以参与子节点的产生选择过程。
解决偏好问题
ID3算法对可取值较多的特征有偏好,C4.5算法使用信息增益比来选择特征,解决偏好问题。信息增益比的定义如下:
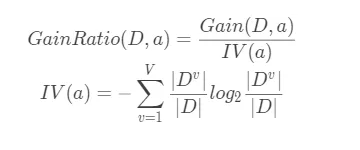
以上定义的符号,大部分在上一部分中已经出现过了,$GainRatio(D,a)$就是将数据集$D$按照特征 $a$进行划分后的信息增益比。通常来说,特征$a$的可取值数目越大,$IV(a)$的值也会越大。将 $IV(a)$放在分母的位置上,在一定程度上减轻了使用信息增益选择特征时,会更加偏好那些可取值数目多的特征带来的不利影响。但是直接使用信息增益比来选择特征则会更加偏好那些可取值数目较少的特征。因此C4.5算法并不是直接选取信息增益比最大的特征,而是采用了以下方式:
- 首先C4.5算法会从可选特征中找出那些信息增益高于平均水平的特征
- 然后再从这些信息增益高于平均水平的特征中选出信息增益比最高的特征
处理缺失值
现实生活中的数据集中的样本通常在某些属性上是有缺失值存在的,如果属性值缺失的样本数量比较少,我们可以直接简单粗暴的把不完备的样本删除掉,但是如果有大量的样本都有属性值的缺失,那么就不能简单地删除,因为这样删除了大量的样本,对于机器学习模型而言损失了大量有用的信息,训练出来的模型性能会受到影响。在决策树中处理含有缺失值的样本的时候,需要解决两个问题:
- 如何在属性值缺失的情况下进行划分属性的选择?(比如“色泽”这个属性有的样本在该属性上的值是缺失的,那么该如何计算“色泽”的信息增益?)
- 给定划分属性,若样本在该属性上的值是缺失的,那么该如何对这个样本进行划分?(即到底把这个样本划分到哪个结点里?)
由于计算过程比较繁琐,不适宜在此类文章中展开叙述,想要了解详细计算过程的朋友可以阅读一下文章:决策树(decision tree)(四)——缺失值处理。
解决过拟合问题
关于过拟合问题是如何解决的,在最后一部分介绍 CART算法会详细的介绍一下剪枝策略。
C4.5算法总结
- C4.5算法解决了ID3算法的偏好问题
- C4.5算法可以处理连续特征
- C4.5算法引入了剪枝策略
- C4.5算法处理了缺失值
- C4.5算法只能用来分类(ID3算法也只能用来分类)
- C4.5算法生成的决策树是多叉树
- C4.5算法处理连续特征时需要排序(排序可能会带来比较大的性能开销)
- C4.5算法执行过程中存在大量的熵运算(ID3算法也存在大量的熵运算)
Desicion Tree(决策树)—Part 3
这部分主要介绍CART算法。
CART算法简介
在ID3算法中我们使用了信息增益来选择特征。在C4.5算法中,使用信息增益比来选择特征。但是ID3算法和C4.5算法都是基于信息论的熵模型的,这里面会涉及大量的对数运算,计算比较复杂。另外ID3算法和C4.5算法生成的决策树都是多叉树,模型比较复杂。CART算法在简化计算的同时也简化了决策树模型:
- 对于回归问题,使用平方误差最小化准则来进行特征选择。对于分类问题,使用基尼指数最小化准则来进行特征选择(CART算法既可以用来解决分类问题,也可以用来解决回归问题)
- CART算法生成的决策树是一棵二叉树
CART算法的特征选择
分类问题
假设数据集$D$中共有$|\gamma|$个类别,第 k 个类别的概率为$p_k$,则数据集$D$的基尼值的定义如下:
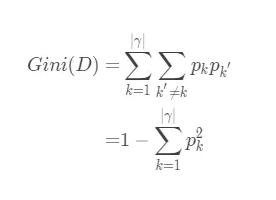
基尼值反映的是从样本集中随机抽两个样本,这两个样本不属于同一类的概率,因此基尼值越小,数据集的纯度越高。
如果根据特征$a$的取值对数据集$D$进行划分,由于CART算法生成的决策树是一棵二叉树,所以就是将数据集$D$根据特征$a$的取值划分为两部分:$D_1,D_2$。则特征 a 对应的基尼指数为:
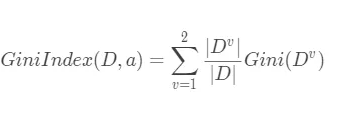
基尼指数代表了模型的不纯度,基尼指数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的.
回归问题
对于回归问题,由于要预测的是连续值,所以需要一个指标对连续值的混乱程度进行度量,这里用均方差来度量样本集上连续值的混乱程度。假设共有$m$个特征,并假设每个特征有若干个候选划分点,遍历每个特征的所有候选划分点将数据集$D$ 划分成$D_1,D_2$两部分,求出使$D_1,D_2$均方差之和最小的特征和其对应的划分点。
CART算法如何划分数据集
连续特征
对于连续特征来说,假设在样本集$D$中连续特征$a$的取值有$n$个,记为:
$${a_1,a_2,a_3,…,a_n}$$
那么对于特征$a$共有$n-1$个候选划分点,首先我们要将这$n$个取值排序。然后通过以下公式计算出这$n-1$个划分点:
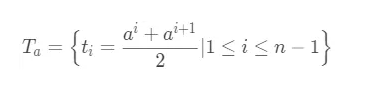
然后按每个候选划分点进行划分,将样本集划分为两部分,一部分中的每个实例对应的特征的值都大于或者等于候选划分点,另一部分中的每个实例对应特征的值则都小于候选划分点。
非连续特征
对于非连续特征来说,就是遍历特征上的每个取值,按照每个取值进行划分,同样将样本集划分为两部分,一部分样本集中的每个实例对应的特征的值等于该取值,另一部分实例对应的特征的值则不等于该取值。
剪枝
剪枝策略主要有两种,分别为预剪枝和后剪枝,剪枝是为了解决过拟合问题。
预剪枝是在决策树的生成过程中,对每个结点在划分前后进行评估。如果当前结点划分后并不能带来泛化能力的提升,就停止划分当前结点,并将当前结点标记为叶结点。
后剪枝是先训练一棵完整的决策树,然后自底向上对每个非叶结点进行考察,若将该结点对应的子树替换为叶子结点能带来决策树泛化能力的提升,则将该子树替换为叶结点。
那如何判断决策树的泛化能力是否提升呢?可以用“留出法”,也就是预留一部分数据用作“验证集”进行评估。
通常来说,后剪枝比预剪枝保留了更多的分支,所以一般情形下,后剪枝更不容易欠拟合。并且通过后剪枝得到的决策树的泛化能力也往往要比预剪枝好。但是后剪枝要在决策树完全生成以后进行,与预剪枝相比时间开销更大。
Expectation Maximization Algorithm(EM算法)
算法原理
EM算法也称期望最大化(Expectation Maximum)算法,它是很多机器学习算法的基础。EM算法只需要有一些训练数据,定义一个最大化函数,经过若干次迭代,我们需要的模型就训练好了。
概率模型有时既含有观测变量,又含有隐变量。对于只含有观测变量的情况,给定观测数据,我们可以直接采用极大似然估计法或贝叶斯估计法估计模型参数。但是,当模型含有隐变量的时候,就无法直接使用这些估计方法估计模型参数了。EM算法就是含有隐变量的模型参数的极大似然估计法
假设我们采集了50个男生、50个女生的身高数据。并且我们知道每条数据对应的是男生还是女生。假设男生的身高服从高斯分布$N(\mu_1,\sigma_1)$,女生的身高服从高斯分布$N(\mu_2,\sigma_2)$,这时候我们可以用极大似然估计法,通过这50个男生和50个女生的身高数据来估计这两个高斯分布的参数。大致步骤如下:
- 写出概率密度函数
- 写出联合概率密度函数
- 得到极大似然函数
- 转化为对数似然函数
- 对各个参数求偏导并令导数为0
- 得到参数估计值
假设我们采集了50个男生、50个女生的身高数据。但是我们不知道每条数据对应的是男生还是女生。假设男生的身高服从高斯分布$N(\mu_1,\sigma_1)$,女生的身高服从高斯分布$N(\mu_2,\sigma_2)$,这时候我们就不可以直接用极大似然估计法来估计这两个高斯分布的参数了。
因为通常来说,我们只有知道了这两个高斯分布的参数我们才能知道每条数据对应的更有可能是男生还是女生。但从另一方面去考量,我们只有知道了每条数据对应的是男生还是女生才能更准确地估计这两个高斯分布的参数。
这里每条数据对应的性别就是隐变量。EM算法就是解决这类问题的。EM算法解决上面这个问题的一般步骤:
- 初始化两个高斯分布的参数值
- E步:基于这两个高斯分布来猜测隐含数据(每条数据对应的性别是男生还是女生)
- M步:基于观测数据和隐含数据一起来极大化对数似然函数,求解并更新两个高斯分布的参数值
- 迭代 2、3 步,直到参数基本无变化,算法收敛
从上面的描述可以看出,EM算法是迭代求解最大值的算法,同时算法在每一次迭代时分为两步:E步和M步。一轮轮迭代更新隐含数据和模型分布参数,直到收敛,即得到我们需要的模型参数。如果只想了解算法的思想,看到这里就基本可以了。
推导过程
极大化含有隐含变量的对数似然函数
对于$m$个样本的观测数据$x = (x^{(1)},x^{(2)},…,x^{(m)},)$,找出模型的参数$\theta$,极大化以下对数似然函数:
$$\theta = \arg \max_\theta\sum_{i=1}^mlogP(x^{(i)}|\theta)$$
如果我们得到的观测数据对应的隐含数据为$z = (z^{(1)},z^{(2)},…,z^{(m)},)$,此时我们要极大化的对数似然函数如下:
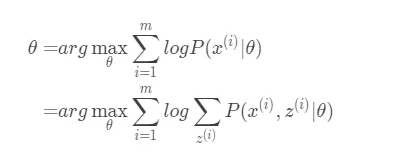
直接通过上式求解$\theta$,主要有以下两个难点:
- 有隐藏变量$z$存在
- 包含和的对数,求偏导比较困难
引入 Q 分布

Jensen不等式

EM算法的一般形式
- 首先我们要初始化参数$\theta$
- 重复以下步骤直到收敛:
- E-Step:对于当前参数$\theta$,找到使
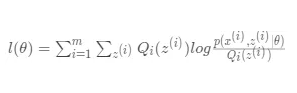
成立的Q 分布,即让$Q_i(z^{(i)}) = p(z^{(i)}|x^{(i)}|\theta)$ - M-step:在M-step中对对数似然函数进行极大似然估计,得到新的参数$\theta$,形式化表述为:

- E-Step:对于当前参数$\theta$,找到使
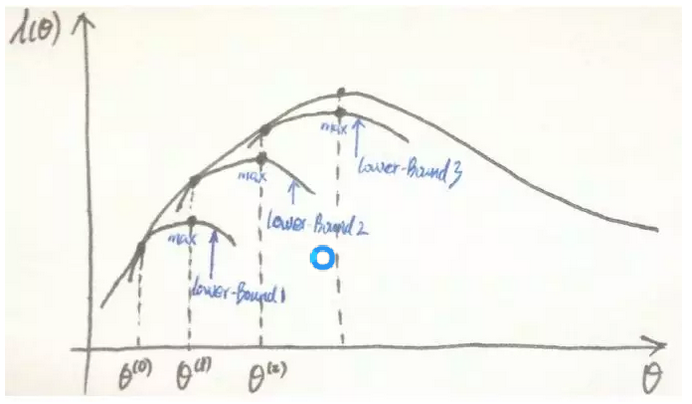
EM算法中的坐标上升过程
如果我们将EM算法的优化目标看成:
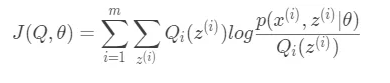
那么EM算法就可以看做是对目标函数的坐标上升过程,在E-step中, $\theta$不变,调整Q使函数变大,在M-step中,Q不变,调整$\theta$使目标函数变大。
EM算法的直观图示
参考
- 李航 —《统计学习方法》
- 周志华 —《机器学习》
- 吴恩达 — 斯坦福机器学习课程
- 张雨石 — 斯坦福ML公开课笔记
- 阮一峰 — 朴素贝叶斯分类器的应用
- 决策树(decision tree)(四)——缺失值处理
- 刘建平 — EM算法原理总结


